| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 리눅스
- 온라인 ddl
- dff
- 스택머신
- ec2
- 밑바닥부터 구현하는 컴퓨팅 시스템
- jack 문법
- s3
- Terraform
- 어뎁티브 해시 인덱스
- 핵심 데이터 모델링
- 필수 스크립트
- 밑바닥부터 만드는 컴퓨팅 시스템
- 핵기계어
- 밑바닥부터 만드는 운영체제
- 안전하게 테이블 변경
- 구문 분석
- innodb구조
- innodb 버퍼풀
- 도커
- vm머신
- InnoDB
- vm번역기
- 운용 시 유용한 쿼리
- nandtotetris
- performance스키마
- 메모리 세그먼트
- 컴퓨터 아키텍쳐
- MySQL
- 마운트
- Today
- Total
이것이 점프 투 공작소
B-Tree 알고리즘 본문
B-Tree란?
B-tree는 Self-balanced Tree 중 가장 유명한 자료구조입니다. Balanced-tree를 의미하며,
이진트리를 확장해 하나의 노드가 가질 수 있는 자식 노드의 최대 숫자가 2보다 큰 트리 구조입니다.
최소차수는 자식수의 하한값을 의미하며, 최소차수가 t라면 M=2t−1을 만족합니다.
최대 M개의 자식을 가질 수 있는 B-Tree를 M차 B-Tree 라고 합니다.
만약 최소차수 t가 2라면 3차 B트리이며, 데이터(key)의 하한은 1개입니다.

B-Tree의 특징
B-Tree는 아래와 같은 특징을 가집니다.
- 노드의 데이터(key)는 항상 정렬된 상태로 저장됩니다.
- 자식 노드의 데이터는 부모 노드의 데이터에 따라 정렬되어 나뉘어집니다.)
- 노드는 최소 M/2-1 ~ M-1개의 데이터(KEY)를 가집니다. (M/2가 소수로 나온다면 올림처리)
- 노드는 최대 M/2 ~ M개의 자식노드를 가집니다. (M/2가 소수로 나온다면 올림처리)
- 내부노드의 데이터가 k개 라면 자식노드의 수는 언제나 k+1개입니다.
- 모든 리프노드의 높이는 같습니다.
B-Tree 탐색 과정
1. 루트 노드에서 탐색 시작합니다.
2. K를 찾았다면 탐색을 종료합니다.
3. K와 노드의 데이터(KEY)를 비교하여 적절한 자식노드로 내려갑니다.
4. 해당 과정을 리프노드에 도달할 때 까지 반복하며 리프노드에서도 K를 찾지 못하면 값이 없다고 판단합니다.
1. 루트 노드에서 탐색을 시작합니다. (K : 46)

2. K는 루트노드 보다 큰 값이기에 왼쪽 자식으로 이동합니다.

3. K는 현재노드의 값들 사이에 있는 값이기에 가운데 자식노드로 이동합니다.

4. 리프노드에서 K을 찾아냅니다. 만약 K가 없다면 찾는 값(K)이 없다고 판단합니다.

B-Tree 데이터 삽입
B-Tree 데이터 삽입은 항상 리프노드에서 시작되며
아래와 같은 순서로 B-Tree에 데이터 삽입이 이루어집니다.
1. 트리가 비어있다면 루트노드를 할당하고 K를 삽입합니다.
2. 트리가 비어있지 않다면, 데이터를 넣을 적절한 리프노드를 탐색합니다.
3. 리프 노드에 데이터를 넣고 리프 노드가 적절한 상태에 있다면 종료한다.
4. 리프 노드가 부적절한 상태에 있다면 분할한다.
추가로 B-Tree에 데이터가 삽입 될 때 상황은 2가지로 나뉘어집니다.
노드가 부적절한 상태가 있어 '분할이 일어나는 경우', 적절한 상태에 있어 '분할이 일어나지 않는 경우' 입니다.
적절한 상태?
B-Tree의 조건(특징)을 위배하지 않는 상태를 의미합니다.
노드를 분할한다?
노드가 가질 수 있는 최대 데이터(KEY) 수(M-1)가 초과되면 가운데 데이터를 기준으로 좌우 데이터를 분할하고 가운데 데이터는 부모 노드로 올립니다.
분할이 일어나지 않는 경우
분할이 일어나지 않는 경우는 간단합니다.
적절한 위치의 노드로 찾아간 다음 데이터를 추가합니다.
1. 먼저 K가 들어갈 리프노드를 탐색합니다. (K : 16) (트리는 3차 B-Tree입니다)

2. K를 추가하여도 해당 리프노드는 적절한 상태에 있기에 그대로 K를 추가합니다.

분할이 일어나는 경우
적절한 위치의 노드로 찾아간 후 데이터가 추가되었을때 노드 분할이 필요 한 경우에는
해당 노드 데이터의 중앙값(median)을 부모 노드로 올립니다.
부모노드에서도 노드 분할이 필요한 경우 동일한 과정을 반복합니다.
1. K가 들어갈 루트노드를 탐색합니다 (K:13) (트리는 3차 B-Tree입니다)

2. 해당 루트노드에 K를 추가합니다.
K가 추가되었을 때 리프노드의 데이터는 최소 데이터 수 (M-1)개를 초과하게 됩니다.
즉 부적절한 상태가 되기에 노드분할을 실시합니다.

3. 노드를 분할하여 중앙값을 부모노드로 올리고 리프노드를 분할합니다.
(만약 해당 작업으로 인해 부모노드가 부적절한 상태가 된다면 동일하게 분할작업을 실시합니다.
B-Tree 데이터 삭제
B-Tree 데이터 삭제 또한 항상 리프노드에서 시작됩니다.
삭제 후 노드의 데이터 수가 최소 데이터수(M/2-1)보다 적어졌다면 트리를 재구조화 합니다.
루트 노드의 데이터 수는 최소 KEY수(M/2-1)를 만족하지 않아도 재구조화 하지 않습니다.
크게 리프노드의 데이터가 삭제 될 때, 내부노드의 데이터가 삭제 될 때로 구분됩니다.
재구조화가 필요한 경우와 재구조화 방법
데이터를 삭제했을때 노드의 '최소 데이터수 (M/2-1)' 보다 작아지게 된다면 트리의 재구조화가 필요합니다.
이럴때 형제, 부모 노드의 값들을 빌려와 재구조화를 진행하게됩니다.
1. 리프노드의 데이터가 삭제 될 때
리프노드의 삭제에서는 삭제 후 노드가 적절한 상태에 있을 때, 적절하기 않고 형제노드의 지원을 받을 수 있을 때
적절하지 않고 형제노드의 지원을 받을 수 없을 때 세가지 경우가 있습니다.
1-1 삭제 후 노드가 적절한 상태에 있어 재구조화가 필요하지 않는 경우
노드에 있는 데이터를 삭제합니다. (추후 별도 작업 X)
1-2 삭제 후 적절한 상태에 있지 않아 재구조화가 필요하고 형제노드의 지원을 받을 수 있는 경우
데이터가 삭제 후 노드가 '최소 데이터수 (M/2-1)'를 만족하지 못한다면 재구조화를 시작합니다.
먼저 노드의 형제노드에서 지원을 받을 수 있는지 확인합니다.
형제노드의 데이터가 여유있다면 **부모노드를 통해서 형제노드의 지원을 받습니다.**
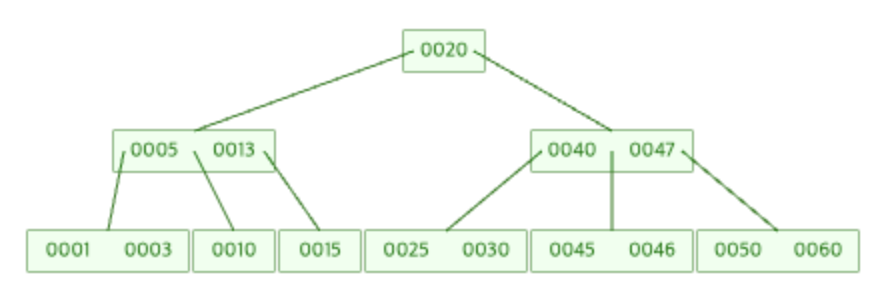
1-2-1 . 삭제할 데이터의 노드로 이동합니다. (K : 50)

1-2-2. 데이터를 삭제하게되면 노드의 '최소 데이터수'를 만족하지 못하기에 데이터가 여유있는 형제노드의 지원을 받습니다.
왼쪽 형제노드가 여유있다면 왼쪽형제 노드에서, 오른쪽 형제노드가 여유있다면 오른쪽 형제 노드에서 지원을 받습니다.
위와 같은 상황에서는 왼쪽 형제노드가 여유있기에 왼쪽 형제 노드에서 부모노드를 통해 지원을 받습니다.
왼쪽 형제노드의 가장 큰 값(46)을 부모 노드로 올리고, 부모노드에서 삭제할 K(50)와 형제노드에서 올라온 값(46) 사이의 값(47)을 K가 있던 노드에 지원받습니다.


1-2-3 삭제 후 적절한 상태에 있지 않아 재구조화가 필요하고 형제노드의 지원을 받을 수 없는 경우 (부모노드의 지원을 받는다)
만약 형제노드가 여유가 없어 지원을 받을 수 없다면, 부모노드의 지원을 받아야합니다.
여기서는 크게 왼쪽 노드가 존재할때 오른쪽 노드와 존재할때 두가지로 구분됩니다.
부모노드의 지원을 받은 후에는 형제노드와 합칩니다.
- 왼쪽 형제 노드가 존재할때
왼쪽 형제 노드가 있다면 왼쪽 형제 노드의 데이터와 나 사이 데이터를 부모노드로 부터 받습니다.
부모로 받은 데이터와 왼쪽 형제 노드의 데이터를 왼쪽 형제 노드에 합칩니다.
나의 노드를 삭제합니다.
- 오른쪽 형제 노드가 존재할때
오른쪽 형제 노드가 있다면 오른쪽 형제 노드의 데이터와 나 사이 데이터를 부모로부터 받습니다.
부모로 받은 데이터와 오른쪽 형제 노드의 데이터를 내 노드에 합칩니다.
오른쪽의 형제 노드를 삭제합니다.
- 만약 부모노드로 부터 지원을 받다가 부모노드가 적절한 상태가 아니개 된다면?
자식노드의 재조정으로 인해 부모노드가 적절한 상태가 아니게 된다면,
자식노드의 재조정 처리 후 부모노드에서도 동일한 재조정 과정을 진행합니다.
만약 그 부모노드가 루트 노드고 적절한 상태가 아니게 되면 부모 노드(루트 노드)를 삭제합니다.
아래 합쳐진 노드가 루트노드가 됩니다.
예를들어 아래와 같은 B-Tree에서 '데이터 5'를 삭제한다면

K 삭제 후 형제노드의 지원을 받아야하지만, 형제 노드가 여유가 없어 부모노드의 지원을 받아야합니다.

아래와 같은 작업을 진행합니다.
1. 왼쪽 형제 노드가 존재하기에 왼쪽 형제 노드의 데이터와 K 사이 데이터(3) 를 부모노드로 부터 받습니다.
2. 부모로 받은 데이터와 왼쪽 형제 노드의 데이터를 왼쪽 형제 노드에 합칩니다.
3. 나의 노드를 삭제합니다.
하지만 부모노드로 부터 값을 받아오게 되니 이번엔 부모노드가 부적절한 상태가 되었습니다.
동일하게 부모노드를 기준으로 부모, 형제 노드로부터 값을 빌려오는 작업을 진행합니다.
리프노드와 동일하게 형제노드가 여유있다면 형제 노드로부터, 여유가 없다면 부모노드로 부터 값을 가져오는 작업을 진행합니다.

부모노드 기준 오른쪽 형제노드의 데이터가 여유가 있기에 형제 노드로부터 값을 가져옵니다.
오른쪽 형제노드의 가장 작은 값(40)을 부모 노드로 올리고, 부모노드에서 사라진 값(3)와 오른쪽 형제노드에서 올라온 값(40) 사이의 값(20)을 지원받습니다.

아래와 같이 재구조화가 완료되었습니다.

2. 내부 노드의 데이터 삭제 시
앞에서는 모두 리프노드에서 데이터가 삭제되는 경우만들 다루었지만
내부 노드에서 데이터가 삭제되는 경우도 존재합니다.
내부노드에서 삭제가 일어나는 경우.
삭제하려는 내부노드를 리프노드의 데이터와 위치를 바꾼 후 리프노드의 삭제 방식과 동일하게 진행합니다.
내부노드와 리프노드의 위치를 변경 할 때는 리프노드는 LMAX, RMIN 두 값중 하나를 선택하여 변경합니다.
- LMAX : 나보다 작은 데이터 중 가장 큰 데이터
- RMIN : 나보다 큰 데이터 중 가장 작은 데이터
아래와 같은 상황의 3차 B-Tree가 있을때
내부노드의 데이터 K (20)을 삭제하겠습니다.

삭제할 데이터 K(20)와 LMAX(3)값의 위치를 변경합니다. (K와 RMIN을 변경해도 상관없습니다)
이후 리프노드에서 K(20)을 삭제합니다.
만약 리프노드에서 K삭제 이후 재구조화가 필요한 상태가 된다면, 리프노드에서의 삭제에서 사용했던 방법과 동일한 방법으로 재구조화를 진행합니다.

아래처럼 재구조화가 완료되었습니다.

'DB' 카테고리의 다른 글
| MySQL 실행계획 보는 방법 (0) | 2024.12.30 |
|---|---|
| MySQL 옵티마이저가 하는 일 (0) | 2024.12.21 |
| InnoDB 아키텍쳐를 알아보자 (0) | 2024.12.12 |
| MySQL엔진의 아키텍쳐를 알아보자 (1) | 2024.12.10 |
| MySQL(InnoDB)의 Lock에 대해 알아보자 (0) | 2024.09.20 |






