RedBlackTree에 대해서 알아보자
RedBlackTree란?

이진 탐색 트리를 사용하다 보면, 데이터들이 불균형하게 생성되는 경우가 있습니다.
불균형한 상태의 이진 트리는 검색효율을 심각하게 저하시키는 원인이 됩니다.
Red Black Tree는 이진트리에 몇가지 규칙들을 더 사용하여 데이터를 균형있게 쌓음으로서, 트리의 높이가 최소한으로 유지되게끔 하여
검색효율을 보장합니다.
균형잡힌 구조 덕분에 Red Black Tree는 시간복잡도 O(LogN)을 유지합니다.
RedBlackTree의 특징
Red Black Tree의 특징은 아래와 같습니다.

- 모든 노드는 빨간색이거나 검은색이다.
- Root노드는 검은색이다
- Leaf노드는 검은색이다.
- 빨간색 노드의 자식들은 모두 검은색이다. (검은색 노드는 빨간색, 검은색 노드 모두 자식으로 가질 수 있다.)
- Root노드와 Leaf노드 사이에 있는 검은색 노드의 수는 모두 동일하다.
그리고 그림을 보면 모든 리프노드가 'NIL'로 되어있는데, 이러한 NIL노드들을 센티넬 노드라고도 합니다.
아무 데이터도 가지고 있지 않지만 색깔만 검은색인 더미 노드를 의미합니다.
구현을 용이하게 만들기 위해 존재하는 노드이며, 규칙 3번을 지키기 위해서 존재하는 노드입니다.
RedBlackTree의 사용처
삽입/삭제가 빈번한 환경에서 뛰어난 성능을 보여줄 수 있습니다.
가장 대표적으로는 리눅스 커널의 CFS (Completetly Fair Scheduler), 즉 공정스케줄러에서 프로세스의 실행시간을 정렬해서 적절하게 cpu에 배분할때도 Red Black Tree를 사용합니다.
또한 자바의 TreeMap과 TreeSet, C++의 STD (std::map, std::set, std::multimap, std::multiset)에서도 키값들이 자동 정렬되는데 내부적으로 RedBlackTree를 사용합니다.
즉 키 기반으로 빠르게 데이터를 넣고, 찾고, 삭제해야 하는 곳에서 유용하게 사용 할 수 있습니다.
RedBlackTree의 높이
h(x)는 x자신으로 부터 leaf노드까지의 가장 긴 간선(edge)의 거리입니다. (트리의 깊이)
bh(x)는 x부터 leaf노드까지의 경로상의 '검은노드의 수'입니다.

RedBlackTree의 4번 규칙에따라 h(x) >= hx(x)가 성립하게되며, (red노드는 Black노드 사이에는 하나밖에 올 수 없기에)
따라서 트리의 최소 노드 수(n)는 n >= 2^bh(x) - 1이라는 식을 만들 수 있습니다.
n ≥ 2^bh(x) - 1그리고 아래와 같은 부등식도 얻을 수 있습니다.
bh(x) ≤ h(x) ≤ 2 × bh(x)
이후 n에 대한 식을 bh(x)에 대한 식으로 변형한다음
n ≥ 2^bh(x) - 1
n + 1 ≥ 2^bh(x)
log₂(n + 1) ≥ bh(x)
부등식에 대입해주면 높이를 구하는 공식을 얻을 수 있습니다.
h(x) ≤ 2 × log₂(n + 1)
구현
Red Black Tree는 기본적으로 이진트리입니다.
따라서 탐색 알고리즘은 이진트리의 알고리즘을 거의 동일하게 사용하면 됩니다.
다만 이진트리의 노드의 삽입, 삭제와 같은 로직에서 Red Black Tree의 규칙을 위배하게되는 상황이 발생하기에 그 무너진 규칙들을 바로잡아주는 과정들이 Red Blakc Tree에 필요합니다.
회전 (Rotate)
Red Black Tree의 규칙을 재정비하기 위한 하나의 방법으로 '회전(rotate)'이 필요합니다.
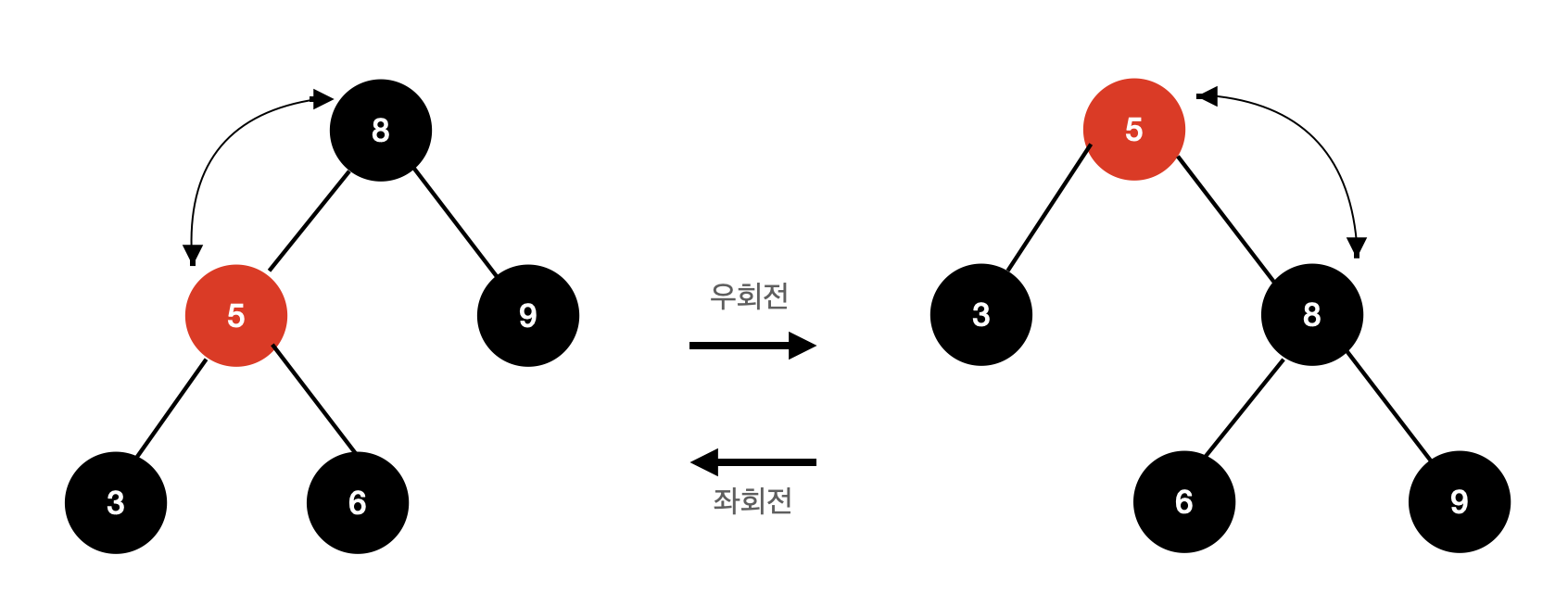
우회전 : 왼쪽자식을 부모의 위치 이동시키면서 우회전, 이후 왼쪽 자식노드의 오른쪽 자식노드를 원래 부모노드의 왼쪽 자식으로 연결합니다.
좌회전 : 오른쪽 자식을 부모의 위치로 이동시키면서 좌회전, 이후 오른쪽 자식노드의 왼쪽 자식노드를 원래 부모노드의 오른쪽 자식으로 연결합니다.
노드 삽입 (Insert)
레드 블랙 트리에 삽입되는 새 노드는 빨간색이어야하고 NIL노드를 새 노드의 양쪽 자식으로 연결해야합니다.
여기서 NIL노드는 모든 레드 블랙 트리의 실제 리프노드에 연결되어있기에, NIL노드에 계속해서 heap공간을 할당하지 않고 하나의 NIL노드를 계속 재활용합니다.

새로운 노드를 삽입하는 과정에서 신경써야하는 레드 블랙 트리의 4번 규칙입니다.
4. 빨간색 노드의 자식들은 모두 검은색이다. (검은색 노드는 빨간색, 검은색 노드 모두 자식으로 가질 수 있다.)
4번 규칙이 위배되는 상황은 '삽입된 노드의 부모가 빨간색'일 떄 발생합니다.
이 경우에 트리의 규칙을 유지하기 위해 색변경과 회전(Rotate)이 필요할 수 있습니다.
만약 삽입된 노드의 부모가 빨간색이라서 트리의 재구성일 필요하다면 재구성 작업 전 추가적으로 몇가지 더 고려해야하는 부분이 있습니다.
- 삼촌노드도 빨간색인 경우
- 삼촌노드가 검은색이며, 새로 삽입한 노드가 부모노드의 오른쪽 자식인 경우
- 삼촌노드가 검은색이며, 새로 삽입한 노드가 부모노드의 왼쪽 자식인 경우
삽입 연산의 모든 예시에서는 부모노드가 조부모노드의 왼쪽 자식이라고 가정합니다.
부모노드가 오른쪽 자식일때는 아래 설명에서 왼쪽과 오른쪽을 바꾸어서 생각하면 됩니다!
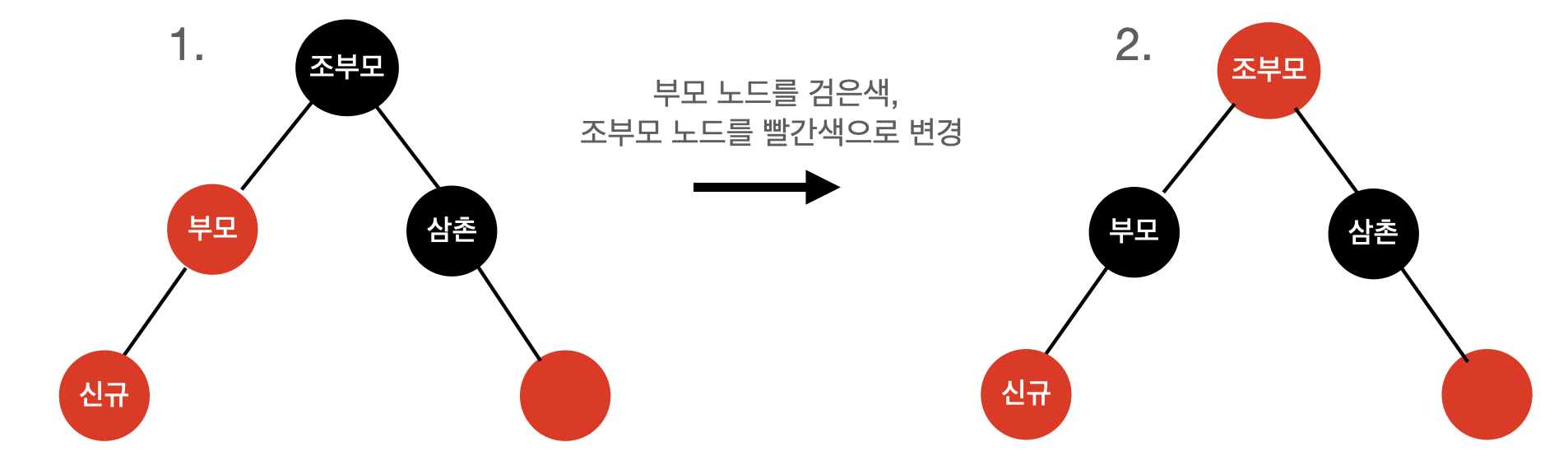
1. 삼촌노드도 빨간색인 경우
- 부모노드와 삼촌노드를 검은색으로 칠하고 조부모 노드를 빨간색으로 칠합니다.
- 빨갛게 칠해진 조부모노드가 다시 4번 규칙을 위배 할 수 있기에 새로 삽입한 노드로 간주하고 다시 트리의 재구성 작업 시행

2. 삼촌노드가 검은색이며 새로 삽입한 노드가 부모노드의 왼쪽 자식인 경우
- 부모 노드를 검은색, 조부모노드를 빨간색으로 칠한 다음 할아버지 노드를 우회전시킵니다.

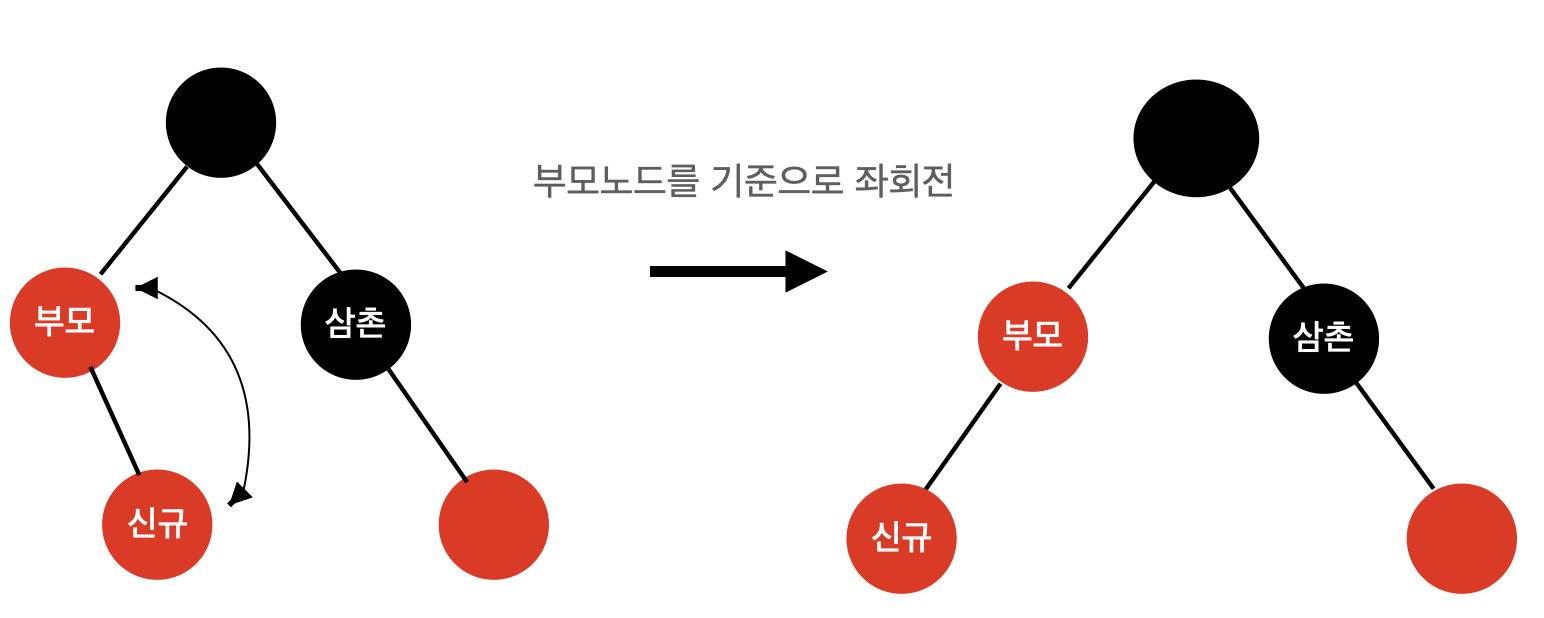
3. 삼촌노드가 검은색이며 새로 삽입한 노드가 부모노드의 오른쪽 자식인 경우
- 부모노드를 좌회전시켜 2번과 동일한 상황으로 만듭니다.
노드 삭제
삭제연산은 삽입에 비해 조금 까다롭습니다.
노드가 삭제되면 왼쪽 자식노드는 부모노드보다 작아야하고, 오른쪽 자식노드듣 부모노드보다 커야한다는 기본적인 이진트리 규칙에 더해
레드 블랙 트리의 규칙을 위한 후속조치도 필요하기 때문입니다.
다행인 부분은 빨간색 노드가 삭제되면 트리의 어떤 규칙도 위배되지 않기에 검은색 노드가 삭제되었을때만 고려하면됩니다.
삭제된 노드가 검은색일때 삭제 연산이 무너뜨릴 수 있는 첫번째 규칙은
5번 'Root노드와 Leaf노드 사이에 있는 검은색 노드의 수는 모두 동일하다' 입니다.
그리고 삭제된 노드의 부모와 자식이 모두 빨간색이면 4번 '빨간색 노드의 자식들은 모두 검은색이다.' 규칙도 위배됩니다.

하지만 4번, 5번 규칙을 지키기 위해 트리는 삭제된 노드를 대체하는 노드를 검은색으로 칠함으로 4번, 5번 규칙을 지킬 수 있습니다.

만약 자식노드가 검은색이라면, 4번 규칙은 위배되지 않고 5번 규칙만 위배됩니다.
하지만 이 경우에도 트리는 대체 노드에 검은색을 칠합니다.
이렇게 검은색이 두번 칠해진 노드를 '이중 흑색 노드'라고 합니다.

이중 흑색 노드가 생기면 1번 규칙 '모든 노드는 빨간색이거나 검은색이다.' 규칙이 무너지게 됩니다.
이를 처리하는 방법은 네 가지 경우로 나뉩니다.
- 형제가 빨간색인 경우
- 형제가 검은색이고 형제의 양쪽 자식이 모두 검은색인 경우
- 형제가 검은색이고 자식은 빨간색, 오른쪽 자식은 검은색인 경우
- 형제가 검은색이고, 형제의 오른쪽 자식이 빨간색인 경우
아래 이중 흑색 노드 처리의 모든 예시에서는 흑색노드가 부모노드의 왼쪽 자식인 경우에 한합니다.
오른쪽 자식인 경우에는 아래 설명에서 왼쪽과 오른쪽을 바꾸어서 생각하면 됩니다!
루트노드가 이중 흑색 노드가 된다면 검은색 노드로 처리합니다.
1. 형제가 빨간색인 경우
- 형제를 검은색, 부모를 빨간색으로 칠합니다.
- 부모를 기준으로 자식노드를 좌회전 시킵니다.
- 아직 이중 흑색 노드는 그대로지만 형제 노드는 검은색으로 바뀝니다.
- 이중 흑색 노드는 '검은색 형제 노드 처리 방법 (2,3,4)' 유형에 맞게 처리합니다.


2. 형제가 검은색이고 형제의 양쪽 자식이 모두 검은색인 경우

- 형제노드를 빨간색으로 칠합니다.
- 이중 흑색 노드가 가지고 있던 검은색을 부모노드에게 넘겨줍니다.
- 부모가 넘겨받은 검은색은 1,3,4 유형에 맞게 처리합니다. (부모노드가 빨간색이면 검은색으로 변경, 검은색이면 이중흑색으로 변경)

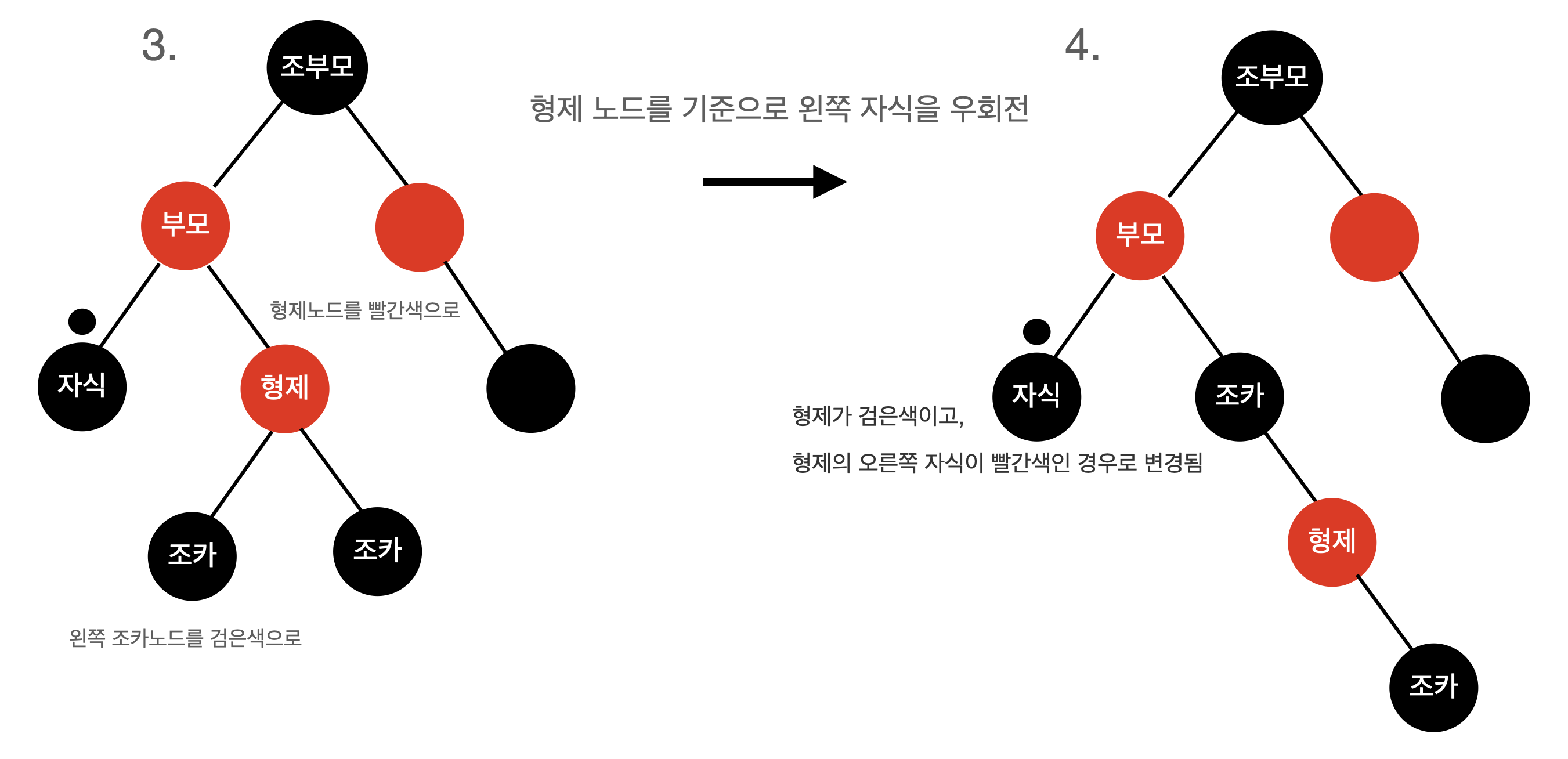
3. 형제가 검은색이고 형제의 왼쪽 자식은 빨간색, 오른쪽 자식은 검은색인 경우

- 형제 노드를 빨간색으로 칠합니다.
- 왼쪽 자식을 검은색으로 칠한다음, 형제 노드를 기준으로 왼쪽 자식을 우회전합니다.
- 이중 흑색 노드는 그대로라면 1,2,4 유형에 맞게 처리합니다.
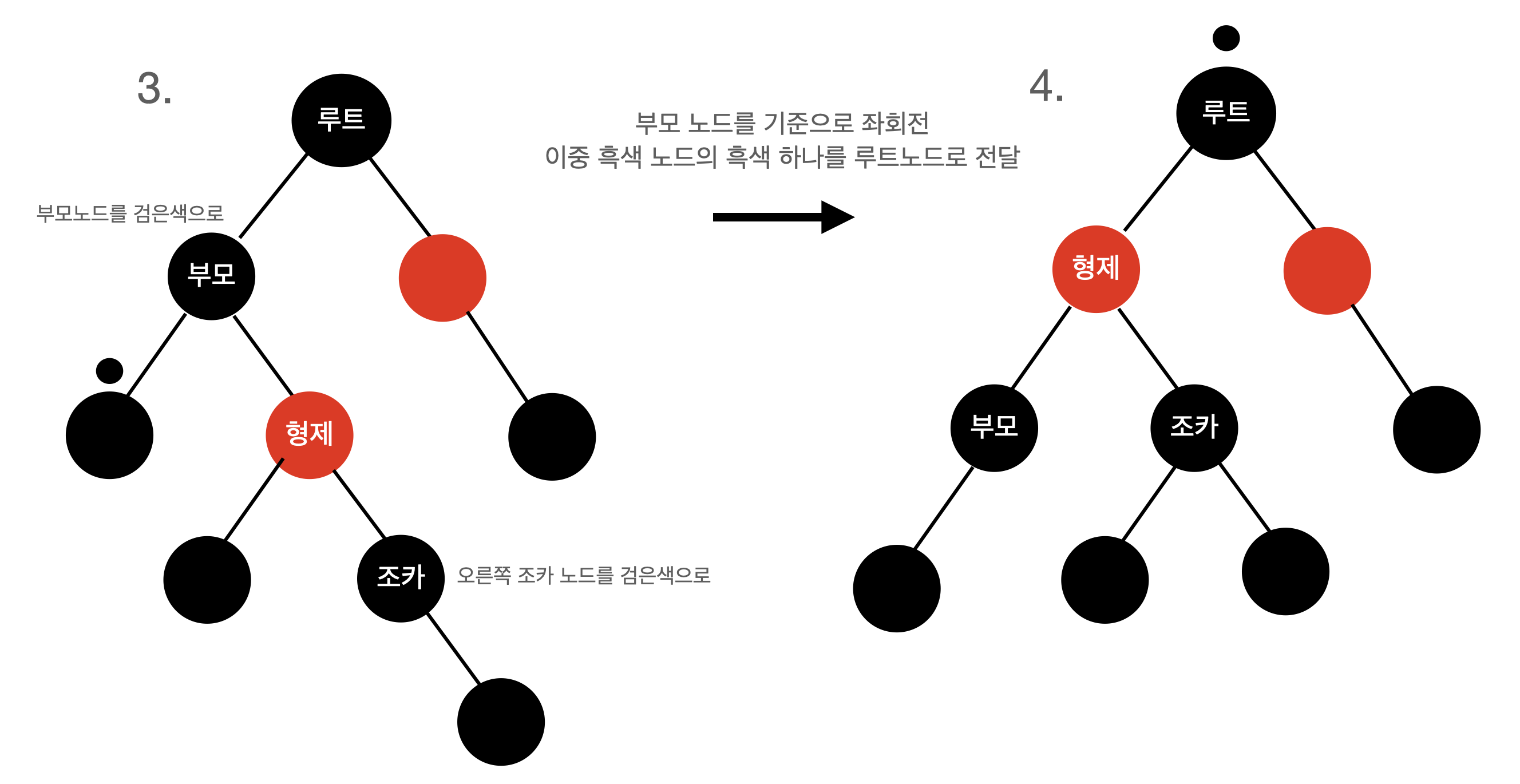
4. 형제가 검은색이고, 형제의 오른쪽 자식이 빨간색인 경우
- 이중 흑색 노드의 부모 노드가 가지고 있는 색을 형제 노드에 칠합니다.
- 부모 노드와 형제 노드의 오른쪽 자식노드를 검은색으로 칠합니다.
- 부모노드를 기준으로 좌회전합니다.
- 이중 흑색 노드의 흑색 하나를 루트노드에 넘겨 이중흑색을 처리합니다. (루트노드는 이중 흑색 노드가 되지 않습니다.)

RedBlackTree 구현 코드 (C)
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
typedef int ElementType;
/*
RedBlackTree 규칙
1.모든 노드는 빨간색이거나 검은색이다.
2.루트노드는 검은색이다
3.리프노드는 검은색이다
4.빨간색 노드의 자식은 모두 검은색이다.
5.리프노드와 루트노드 사이에 있는 검은색 노드의 수는 모두 동일하다
*/
typedef struct tagRBTNode {
struct tagRBTNode* Parent;
struct tagRBTNode* Left;
struct tagRBTNode* Right;
enum {RED, BLACK} Color;
ElementType Data;
} RBTNode;
RBTNode* Nil;
/* 노드 생성 */
RBTNode* RBT_CreateNode(ElementType NewData){
RBTNode* NewNode = (RBTNode*)malloc(sizeof(RBTNode));
NewNode->Parent = NULL;
NewNode->Left = NULL;
NewNode->Right = NULL;
NewNode->Data = NewData;
NewNode->Color = BLACK;
return NewNode;
}
/* 노드 삭제 */
void RBT_DestroyNode(RBTNode* Node) {
free(Node);
}
/* 트리 삭제 */
void RBT_DestroyTree(RBTNode* Tree) {
if (Tree->Right != Nil){
RBT_DestroyTree(Tree->Right);
}
if (Tree->Left != Nil){
RBT_DestroyTree(Tree->Left);
}
Tree->Left = Nil;
Tree->Right = Nil;
RBT_DestroyNode(Tree);
}
/* 노드 찾기 */
RBTNode* RBT_SearchNode(RBTNode* Tree, ElementType Target){
if (Tree == Nil) return NULL;
if (Tree->Data > Target) {
return RBT_SearchNode(Tree->Left, Target);
}
else if (Tree->Data < Target){
return RBT_SearchNode(Tree->Right, Target);
}else {
return Tree;
}
}
/* 작은노드 찾기 */
RBTNode* RBT_SearchMinNode(RBTNode* Tree){
if (Tree == Nil) {
return NULL;
}
if (Tree->Left == Nil) return Tree;
else {
return RBT_SearchMinNode(Tree->Left);
}
}
/* 우회전 */
void RBT_RotateRight(RBTNode** Root, RBTNode* Parent) {
RBTNode* LeftChild = Parent->Left;
Parent->Left = LeftChild->Right; // 왼쪽 자식노드 자리에 왼쪽 자식노드의 오른쪽 자식노드 세팅
// 왼쪽 자식노드의 오른쪽 자식노드의 부모노드를, 왼쪽 자식노드의 부모노드로 세팅
if (LeftChild->Right != Nil){
LeftChild->Right->Parent = Parent;
}
// 왼쪽 자식노드의 부모노드를 부모노드의 부모노드로 세팅 (추후 왼쪽 자식노드가 부모노드가 되어야하기에, 할아버지 노드가 없으면 Root로)
LeftChild->Parent = Parent->Parent;
if (Parent->Parent == NULL) {
(*Root) = LeftChild;
}else { // 부모노드가 할아버지 노드의 왼쪽에 있으면
if (Parent == Parent->Parent->Left){
Parent->Parent->Left = LeftChild; // 왼쪽 자식노드를 부모노드 자리에 위치 (rotate)
}else { // 부모노드가 할아버지 노드의 오른쪽에 있으면
Parent->Parent->Right = LeftChild; // 왼쪽 자식노드를 부모노드 자리에 위치 (rotate)
}
}
LeftChild->Right = Parent; // 왼쪽 자식노드(현재 부모노드 위치)의 오른쪽 자식노드를 오른쪽으로 옮김
Parent->Parent = LeftChild; // 옮겨진 노드의 부모노드를 왼쪽 자식노드(현재 부모노드 위치)로 변경
}
/* 좌회전 */
void RBT_RotateLeft(RBTNode** Root, RBTNode* Parent) {
RBTNode* RightChild = Parent->Right;
Parent->Right = RightChild->Left; // 오른쪽 자식노드(R)의 왼쪽 자식노드(A)를 부모노드(P)의 오른쪽 자식으로 변경
if (RightChild->Left != Nil) {
RightChild->Left->Parent = Parent; // 오른쪽 자식노드(R)의 왼쪽 자식노드(A)의 부모를 P로 설정
RightChild->Parent = Parent->Parent; // P의 부모(G)를 R의 부모로 지정
}
// G의 자식을 R로 설정
if (Parent == Parent->Parent->Left) {
Parent->Parent->Left = RightChild;
}else {
Parent->Parent->Right = RightChild;
}
RightChild->Left = Parent; // P를 R의 왼쪽 자식으로 설정
Parent->Parent = RightChild; // P의 부모를 R로 설정
}
/*이진 탐색의 InsertNode역할을 수행 */
void RBT_InsertNodeHelper(RBTNode** Tree, RBTNode* NewNode) {
if ((*Tree) == NULL) {
(*Tree) = NewNode;
}
if ((*Tree)->Data < NewNode->Data){
if ((*Tree)->Right == Nil) {
(*Tree)->Right = NewNode;
NewNode->Parent = (*Tree);
}else {
RBT_InsertNodeHelper(&(*Tree)->Right, NewNode);
}
}
else if ((*Tree)->Data > NewNode->Data) {
if ((*Tree)->Left == Nil) {
(*Tree)->Left = NewNode;
NewNode->Parent = (*Tree);
}else {
RBT_InsertNodeHelper(&(*Tree)->Left, NewNode);
}
}
}
/* 노드 삽입 후 규칙 복구 */
void RBT_RebuildAfterInsert(RBTNode** Root, RBTNode* X) {
// 빨간색노드의 자식은 반드시 검은색이어야 한다는 규칙 위배
while (X != (*Root) && X->Parent->Color == RED) {
// 부모 노드가 할아버지 노드의 왼쪽 자식인 경우
if (X->Parent == X->Parent->Parent->Left){
RBTNode* Uncle = X->Parent->Parent->Right;
// 1. 삼촌노드가 빨간색인 경우
// 부모노드와 삼촌노드를 검은색으로 칠하고, 할아버지노드를 빨간색으로 변경합니다.
// 할아버지 노드가 변경되었으니 할어버지 노드를 자식노드로 취급하여 재점검 시행
if (Uncle->Color == RED) {
X->Parent->Color = BLACK;
Uncle->Color = BLACK;
X->Parent->Parent->Color = RED;
X = X->Parent->Parent;
}
// 삼촌노드가 검은색인 경우
else
{
// 2. 삼촌노드가 검은색이며 새로 삽입한 노드가 부모노드의 오른쪽 자식인 경우
// 부모노드를 좌회전시켜 상황을 3의 경우와 같게 만듭니다.
if (X == X->Parent->Right) {
X = X->Parent;
RBT_RotateLeft(Root, X);
}
// 3. 삼촌노드가 검은색이며 새로 삽입한 노드가 부모노드의 왼쪽 자식인 경우
// 부모노드를 검은색, 조부모 노드를 빨간색으로 칠한 뒤 조부모노드를 우회전 시킵니다.
X->Parent->Color = BLACK;
X->Parent->Parent->Color = RED;
RBT_RotateRight(Root, X->Parent->Parent);
}
}else { // 부모 노드가 할아버지 노드의 오른쪽 자식인 경우
RBTNode* Uncle = X->Parent->Parent->Left;
if (Uncle->Color == RED){
X->Parent->Color = BLACK;
Uncle->Color = BLACK;
X->Parent->Parent->Color = RED;
X = X->Parent->Parent;
}
else {
if (X==X->Parent->Left){
X = X->Parent;
RBT_RotateRight(Root, X);
}
X->Parent->Color = BLACK;
X->Parent->Parent->Color = RED;
RBT_RotateLeft(Root, X->Parent->Parent);
}
}
}
(*Root)->Color = BLACK; // 루트노드는 항상 검은색
}
/* 노드 삽입 */
void RBT_InsertNode(RBTNode** Tree, RBTNode* NewNode) {
RBT_InsertNodeHelper(Tree, NewNode); // 이진탐색트리의 노드 삽입
NewNode->Color = RED; // 새로운 노드는 빨간색으로 칠하고 Nil을 양쪽 지식으로 연결합니다.
NewNode->Left = Nil;
NewNode->Right = Nil;
RBT_RebuildAfterInsert(Tree, NewNode); // 무너진 Red-Black Tree 규칙 고치기 (빨간삭 노드의 자식들은 모두 검은색이다.)
}
/* 노드 삭제 후 규칙 복구 */
void RBT_RebuildAfterReMove(RBTNode** Root, RBTNode* Successor){
RBTNode* Sibling = NULL;
while (Successor->Parent != NULL && Successor->Color == BLACK)
{
if (Successor == Successor->Parent->Left) {
Sibling = Successor->Parent->Right;
if (Sibling->Color == RED) {
Sibling->Color = BLACK;
Successor->Parent->Color = RED;
RBT_RotateLeft(Root, Successor->Parent);
}else {
if (Sibling->Left->Color == BLACK && Sibling->Right->Color == BLACK){
Sibling->Color = RED;
Successor = Successor->Parent;
}else {
if (Sibling->Left->Color == RED){
Sibling->Left->Color = BLACK;
Sibling->Color = RED;
RBT_RotateRight(Root,Sibling);
Sibling = Successor->Parent->Right;
}
Sibling->Color = Successor->Parent->Color;
Successor->Parent->Color = BLACK;
Sibling->Right->Color = BLACK;
RBT_RotateLeft(Root, Successor->Parent);
Successor = (*Root);
}
}
}else {
Sibling = Successor->Parent->Left;
if (Sibling->Color == RED) {
Sibling->Color = BLACK;
Successor->Parent->Color = RED;
RBT_RotateRight(Root, Successor->Parent);
}else {
if (Sibling->Right->Color == BLACK && Sibling->Left->Color == BLACK){
Sibling->Color = RED;
Successor = Successor->Parent;
}else {
if (Sibling->Right->Color == RED){
Sibling->Right->Color = BLACK;
Sibling->Color = RED;
RBT_RotateLeft(Root, Sibling);
Sibling = Successor->Parent->Left;
}
Sibling->Color = Successor->Parent->Color;
Successor->Parent->Color = BLACK;
Sibling->Left->Color = BLACK;
RBT_RotateRight(Root, Successor->Parent);
Successor = (*Root);
}
}
}
}
Successor->Color = BLACK;
}
/* 노드 삭제 */
RBTNode* RBT_RemoveNode( RBTNode** Root, ElementType Data) {
RBTNode* ReMoved = NULL;
RBTNode* Successor = NULL; // Successor는 ReMoved의 자식 노드 중에서 부모와 연결할 대체 노드를
RBTNode* Target = RBT_SearchNode((*Root), Data);
if (Target == NULL) return NULL;
if (Target->Left == Nil || Target->Right == Nil) {
ReMoved = Target;
}
else {
ReMoved = RBT_SearchMinNode(Target->Right); // MinNode를 ReMoved로 지정 (기본 트리구조 유지를 위해)
Target->Data = ReMoved->Data; // MinNode의 데이터로 Target의 데이터를 변경
}
// 삭제될 노드의 후임자(Successor) 찾기
if (ReMoved->Left != Nil) {
Successor = ReMoved->Left;
}else {
Successor = ReMoved->Right;
}
if (Successor != Nil) {
Successor->Parent = ReMoved->Parent;
}
if (ReMoved->Parent == NULL){
(*Root) = Successor;
}else {
if (ReMoved == ReMoved->Parent->Left){
ReMoved->Parent->Left = Successor;
}else {
ReMoved->Parent->Right = Successor;
}
}
if (ReMoved->Color == BLACK){
RBT_RebuildAfterReMove(Root, Successor);
}
return ReMoved;
}
void RBT_PrintTree(RBTNode* Node, int Depth, int BlackCount) {
int i = 0;
char c = 'X';
int v = -1;
char cnt[100];
if (Node == NULL || Node == Nil) {
return;
}
if (Node->Color == BLACK) BlackCount++;
if (Node->Parent != NULL) {
v= Node->Parent->Data;
if (Node->Parent->Left == Node) c = 'L';
else c='R';
}
if (Node->Left == Nil && Node->Right == Nil) {
sprintf(cnt, "========= %d", BlackCount);
}else {
strncpy(cnt, "", sizeof(cnt));
}
for (i = 0; i<Depth; i++) printf(" ");
printf("%d %s [%c, %d] %s \n", Node->Data, (Node->Color == RED)?"RED":"BLACK", c, v, cnt);
RBT_PrintTree(Node->Left, Depth+1, BlackCount);
RBT_PrintTree(Node->Right, Depth+1, BlackCount);
}
int main(void) {
RBTNode* Tree = NULL;
RBTNode* Node = NULL;
Nil = RBT_CreateNode(0);
Nil->Color = BLACK;
while (1)
{
int cmd = 0;
int param = 0;
char buffer[10];
printf("Enter command number : \n");
printf("(1) Create a node, (2) ReMove a node, (3) Search a Node \n");
printf("(4) Display Tree (5) quit \n");
printf("command number : ");
fgets(buffer, sizeof(buffer)-1, stdin);
sscanf(buffer, "%d", &cmd);
if (cmd < 1 || cmd > 5){
printf("Invalid command Number: \n");
continue;
}
else if (cmd == 4){
RBT_PrintTree(Tree,0,0);
printf("\n");
continue;
}
else if (cmd == 5){
break;
}
printf("Enter the parameter (1~200) :\n");
fgets(buffer, sizeof(buffer)-1, stdin);
sscanf(buffer, "%d", ¶m);
if (param < 1 || param > 200) {
printf("Invalid parameter : %d \n", param);
continue;
}
switch(cmd) {
case 1:
RBT_InsertNode(&Tree, RBT_CreateNode(param));
break;
case 2:
Node = RBT_RemoveNode(&Tree, param);
if (Node == NULL){
printf("not found node to delete : %d", param);
}else {
RBT_DestroyNode(Node);
}
break;
case 3:
Node = RBT_SearchNode(Tree, param);
if (Node == NULL) {
printf("Not found Node :%d \n", param);
}else {
printf("Found Node : %d(Color:%s) \n", Node->Data, (Node->Color == RED)?"RED":"BLACK");
}
break;
}
printf("\n");
}
RBT_DestroyTree(Tree);
return 0;
}